Mi hermana tiene 9 años. Ella es fascinante y muy inteligente. Le encanta leer, escribir, diseñar vestidos, crear sus propios noticieros y pasarelas, pintar, dibujar, así como declamar a voz potente por toda la casa.
Durante esta cuarentena, ha sido algo complicado que tenga entusiasmo por aprender matemáticas. Comprendo muy bien que sus gustos se centren en el arte y la escritura, sin embargo, creo que es fundamental que tenga una base sólida en matemáticas, no solo para fines académicos, sino para la vida.
Me he dado a la tarea de enseñarle esta bonita ciencia, de forma independiente y con mis métodos.

Hoy me platicó que vió en un video que un famoso recreó Las Vegas en su casa. De inmediato, una vocecita interna me gritó: aprovecha la oportunidad para enseñarle una lección.
Así que, decidí hacer nuestra propia versión de Las Vegas.

Hace tiempo compré mi propio set de dados de calabozos y dragones. Lo que me llamó la atención es tener dados con distinto número de caras, distinto número de probabilidades. De algo me servirían algún día. Así que hoy, desempolvé mis dados y le propuse un juego a mi hermana:
Tengo 7 dados:
1 dado de 4 caras
1 dado de 6 caras
1 dado de 8 caras
2 dados de 10 caras
1 dado de 12 caras
1 dado de 20 caras
Todos los dados tienen números del 1 al número de caras que poseen. Para jugar, debes apostar 1 peso. Si tu apuestas a un número que esté en los siguientes rangos y alguno de los dados cae con ese número, obtendrías:
Eliges un número 13 al 20 obtienes 10 pesos
Eliges un número 11 al 12 obtienes 7 pesos
Eliges un número 9 al 10 obtienes 4 pesos
Eliges un número 7 al 8 obtienes 3 pesos
Eliges un número 5 al 6 obtienes 2 pesos
Eliges un número 1 al 4 obtienes 1.5 pesos
¿Ahora bien, que harían ustedes? ¿Que escenario sería el mejor para apostar?
Debo reconocer, el escenario suena un poco enredoso ( para ser sincero, fue a propósito).
Vamos a desentrañarlo poco a poco con ejemplos:
Supongamos que apuestas al 8.
Solo 5 dados ( 1 de 8 caras, 2 de 10 caras, 1 de 12 caras, 1 de 20 caras) van a tener el número 8. Al haber menos dados, sabemos que, evidentemente las probabilidades de ganar son menores, por ello la casa recompensa con más dinero si atinas ( 3 pesos!).
Recordemos que para ganar, al menos 1 de los dados debe salir en 8.
¿Sabiendo esto, como evaluamos que situación nos dá mejor beneficio? Beneficio, decisiones. Este inocente juego esconde una lección de matemáticas y economía.
Consideraciones primordiales
Empecemos por el principio. Definamos algunas nociones obvias que nos ayudarán a entender el mejor el problema a priori.
- La suma de probabilidades de un evento dado, deben dar como suma 1.
- Al lanzar un dado de N caras, tenemos una probabilidad de obtener un resultado correcto de p = 1/N.
- La probabilidad de No obtener el resultado deseado es:
q = (N-1)/N - El lanzado de cada dado es un evento independiente. El resultado de un dado no afecta a los otros dados. De este enunciado se puede derivar que, para dos eventos independientes, la probabilidad de que caiga X en ambos dados estaría dada por:
P(X1 ^ X2) = P(X1) * P(X2)
El símbolo ^ aquí representa y (and).
¿Entonces, teniendo distintos dados, como podemos calcular la probabilidad combinada de estos dados, para obtener al menos una vez el número que queremos?
Imaginemos que tenemos 2 dados, con caras N1 y N2.
Podemos decir que, la situación que queremos se puede decir como:
La probabilidad de que caiga el número X en el dado 1, o si no cae X en el dado 1, considerar la probabilidad de que caiga X en el dado 2.
Si lo representáramos en un diagrama, las probabilidades quedarían como:
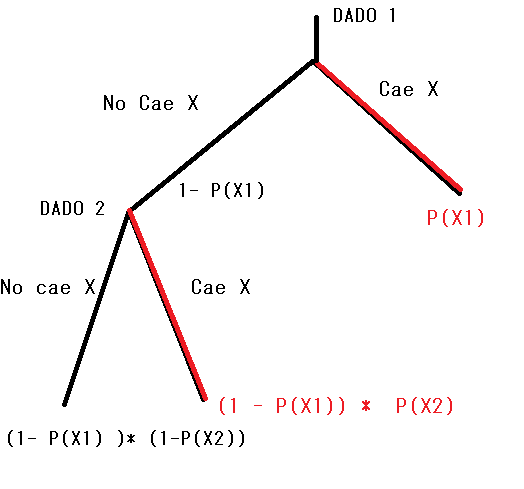
Haciendo uso de ecuaciones, la probabilidad de los dos dados quedaría como:
P(X1 | X2) = P(X1) + (1-P(X1)) * P(X2)
Que podemos entender como:
- P(X1 | X2) : La probabilidad de que caiga X en d1 o en d2.
- P(X1) : La probabilidad de que caiga X en d1.
- (1-P(X1)) * P(X2): La probabilidad de si no cae X en el dado 1, considerar que caiga X en el dado 2.
El símbolo | significa en este caso: o (or)
Observese que, no importa el orden de X1 o X2, la ecuación funciona en ambas formas. Otra forma de interpretar esta misma ecuación sería ( reacomodando términos):
P(X1 | X2) = P(X1) + P(X2) - P(X1) * P(X2)
La probabilidad de que caiga X en d1 o d2 está dada por la probabilidad de que X caiga en 1, o que caiga en 2, pero no en ambos a la vez.
Observe que, el evento X1 | X2 puede ser evaluado e interpretado como un solo evento ( sí, compuesto por otros 2 eventos más sencillos). Por ende, podríamos renombrarlo con otra etiqueta, si lo deseáramos y más importante, podemos aplicar esta misma regla para conjugar eventos más complejos como si se trataran de eventos individuales.
Imaginemos ahora que queremos añadir un tercer dado al juego, y que los 3 dados poseen el número que elegimos para la apuesta.
Podríamos hacer nuestro árbol de decisiones una vez más, si así lo deseamos.
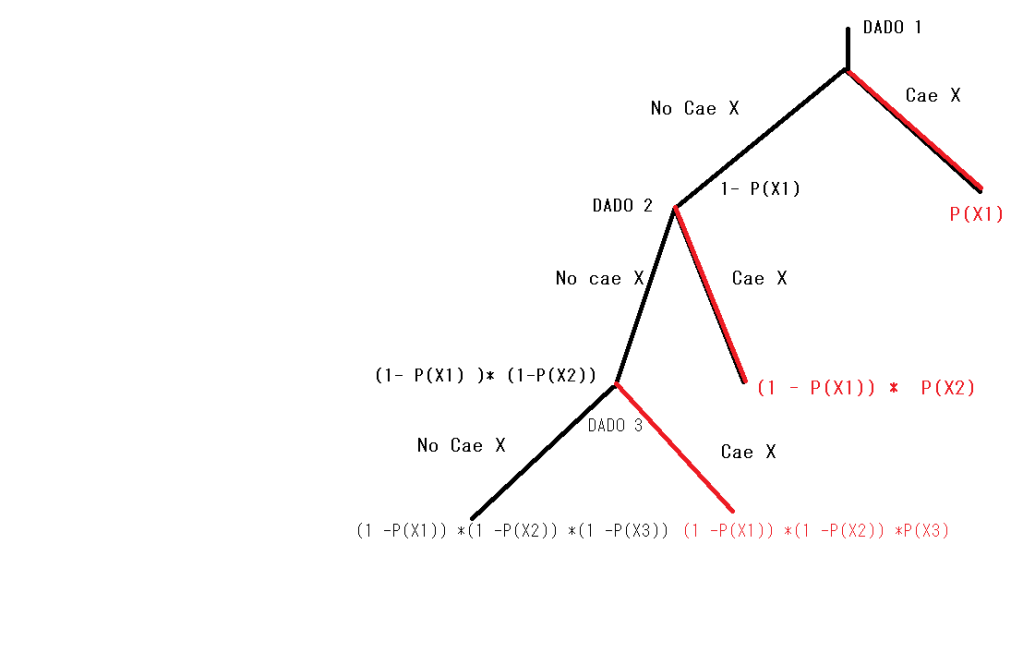
Ahora bien, este diagrama se está haciendo cada vez más grande y me estoy comenzando a hacer bolas. ¿No podemos tomar un atajo?
Claro que si. Como podemos observar, el evento del que deseamos calcular, es que X caiga en el dado 1 o en el dado 2 o en el dado 3.
P(X1 | X2 | X3)
Obsérvese que ya sabemos P(X1 | X2 ) e incluso definimos que el evento Y = X1 | X2 puede ser renombrado.
Nos quedaría como:
### P(Y | X3) = P(Y) + (1-P(Y)) * P(X3)
Sustituyendo Y = X1 | X2
P(X1 | X2 | X3) = P(X1 | X2) + (1-P(X1 | X2)) * P(X3)
Esta conclusión es genial, no solo por lo elegante y intuitiva que resulta la ecuación de probabilidades, sino que, además, nos reduce la cantidad de cálculos, en caso que tomáramos los eventos por separado.
Si desplegamos nuestra ecuación queda como:
P(X1 | X2 | X3) = P(X1) + P(X2) + P(X3) - P(X1)P(X2) - P(X1)P(X3) - P(X2)P(X3)
+ P(X1)P(X2)P(X3)
Y se pone peor, para 5 dados, la ecuación explicita de probabilidad de que caiga X en al menos 1 dado queda como:
P(X1 | X2 | X3 | X4 | X5) = P(X1) + P(X2) + P(X3) + P(X4) + P(X5) - P(X1)P(X2)
- P(X1)P(X3) - P(X1)P(X4) - P(X1)P(X5) - P(X2)P(X3)
- P(X2)P(X4) - P(X2)P(X5) - P(X3)P(X4) - P(X3)P(X5)
- P(X4)P(X5) + P(X1)P(X2)P(X3) + P(X1)P(X2)P(X4)
+ P(X1)P(X2)P(X5) + P(X1)P(X3)P(X4) + P(X1)P(X3)P(X5)
+ P(X1)P(X4)P(X5) + P(X2)P(X3)P(X4) + P(X2)P(X3)P(X5)
+ P(X2)P(X4)P(X5) + P(X3)P(X4)P(X5) -P(X1)P(X2)P(X3)P(X4)
- P(X1)P(X2)P(X3)P(X5) - P(X1)P(X2)P(X4)P(X5)
- P(X1)P(X3)P(X4)P(X5) - P(X2)P(X3)P(X4)P(X5)
+ P(X1)P(X2)P(X3)P(X4)P(x5)
AAAAAAAAAHHHHHH
Volviendo a nuestra ecuación ### obtenemos que, para un evento compuesto, podemos tomarlo como un evento simple para calcular una nueva probabilidad.
P( Y | X ) = P(Y) + ( 1- P(Y) ) * P(X)
Ahora que, tenemos el conocimiento adecuado, podemos sumergirnos en el problema.
Resolviendo el problema
Para los números del 13 al 20, solo hay un dado que posee alguna de esas caras. La probabilidad de ganar (G1) es entonces,
P(G1) = P(X1) = 1/20
Para los números del 11 al 12, hay dos dados ( 1 de 12 caras, 1 de 20 caras) con alguna de esas caras. La probabilidad de ganar (G2), es:
P(G2) = P(X1|X2) = (1/20) + (19/20)*(1/12) = 31 / 240 ~= 1/8
Para los números del 9 al 10, hay cuatro dados ( 2 de 10 caras, 1 de 12 caras, 1 de 20 caras) con alguna de esas caras. La probabilidad de ganar (G3), es:
P(G3) = P(X1 | X2 | X3 | X4) = P(G2 | (X3 | X4)) = (1/8) + (7 / 8)(19/100) = 233/800 ~= 3/10
(Obsérvese que, en el caso anterior, consideré ya los 2 dados de 10 caras, como un único evento compuesto).
Para los números del 7 al 8, hay cinco dados ( 1 de 8 caras, 2 de 10 caras, 1 de 12 caras, 1 de 20 caras) con alguna de esas caras. La probabilidad de ganar (G4), es:
P(G4) = P(G3| X5) = (3/10) + (7 / 10)(1/8) = 31/80 ~= 3/8
Para los números del 5 al 6, hay seis dados ( 1 de 6 caras, 1 de 8 caras, 2 de 10 caras, 1 de 12 caras, 1 de 20 caras) con alguna de esas caras. La probabilidad de ganar (G5), es:
P(G5) = P(G4| X6) = (3/8) + (5/8)(1/6) = 23/48 ~= 1/2
Para los números del 1 al 4, los 7 dados tienen esa cara. La probabilidad de ganar (G6), es:
P(G6) = P(G5| X7) = (23/48) + (25/48)*(1/4) = 117/192 ~= 5/8
Genial! ya tenemos las probabilidades de cada uno de los escenarios. Ahora bien, podemos concluir que, ¿La mejor situación, es aquella donde tengo mejor posibilidad?
No exactamente. La probabilidad es determinante. Sin embargo, en cada escenario tenemos ganancias distintas. Evaluemos entonces, en que situación podríamos ganar más dinero. Para hacerlo, imaginemos lo siguiente.
Consideremos M juegos, donde M es un número muy grande.
- Si jugamos M veces, probabilísticamente ganaremos M * P(G1) veces, y ganaremos Q(1) pesos.
- En M casos, perderemos 1 peso.
Por ende, la ganancia final Z, luego de jugar M veces sería:
Z(1) = M * P(G1) *Q(1) - M = M * (P(G1) *Q(1) -1 )
Z(1) = M * P(G1) *Q(1) – M
Ganancia final lo que obtienes menos lo que gastas.
Nosotros queremos una máxima ganancia, por lo que hay que calcular y comparar cada una de las situaciones.
Ganancia al elegir 13 – 20:
Z(1) = M * ( (1/20)*10 -1 ) = - 1/2 * M => Z(1) /M = - 1/2
Ganancia al elegir 11 – 12:
Z(2) = M * ( (1/8)*7 -1 ) = - 1/8 * M => Z(2) /M = - 1/8
Ganancia al elegir 9 – 10:
Z(3) = M * ( (3/10)*4 -1 ) = + 1/5 * M => Z(3) /M = + 1/5
Ganancia al elegir 7 – 8:
Z(4) = M * ( (3/8)*3-1 ) = + 1/8 * M => Z(4) /M = + 1/8
Ganancia al elegir 5 – 6:
Z(5) = M * ( (1/2)*2 -1 ) = 0 => Z(5) /M = 0
Ganancia al elegir 1 – 4:
Z(6) = M * ( (5/8)*1.5 -1 ) = - 1/16 * M => Z(6) /M = - 1/16
Obsérvese que, la ganancia probable por juego (Z / M), es constante! Nótese que, en algunos casos, la ganancia por juego es positiva, negativa o incluso cero.
Pero que significa esta cantidad para nosotros?Significa que, luego de haber jugado muchas veces, se prevee que hayamos ganado (Z / M) veces dicha cantidad de dinero.
- Si (Z / M) es negativa, significa que luego de muchos juegos, perderemos dinero.
- Si (Z / M) es positiva, luego de muchas apuestas, es probable que netamente ganemos dinero.
- Si (Z / M) es 0, significa que, luego de muchos juegos, no habremos ganado ni perdido dinero.
Obsérvese que (Z / M) nos determina que tanto podemos ganar o perder luego de varios juegos.
Si elegimos elegimos el caso con el mayor valor de (Z / M), habremos maximizado nuestra ganancia!
Por ende, en esta situación, al elegir números del 7 al 10 era más probable que, luego de unos cuantos juegos, nos retiráramos con ganancia.
El mejor caso, era elegir 9 o 10.
A pesar de que en caso de elegir 13 – 20 teníamos una mayor ganancia al acertar, ( 10 ) al final terminaríamos perdiendo dinero ( más dinero que en cualquier otro caso!).
Además, en el caso de elegir 1 – 4, aunque teníamos una mayor probabilidad de ganar ( probabilidad de 62%!!!) al final, terminaríamos también perdiendo dinero!
Este pequeño juego, nos demuestra la importancia de saber matemáticas para tomar nuestras decisiones. Además, los escenarios que podrían parecer a priori, más adecuados, observamos que puede que no lo sean.
En los casinos y situaciones reales de apuestas, JAMÁS tendrás un coeficiente positivo en tus ganancias por juego (Z/M). Todos los juegos son diseñados para que, en promedio luego de muchas rondas, la case gane.
La casa siempre gana. He aqui el secreto.
Mi padre me dijo que no me complicara, tomara un dado y le enseñara probabilidad así a mi hermana. Luego de que le mostré estas conclusiones se mostró muy interesado en mi juego. Este tipo de situaciones son estudiadas en Teoría de Juegos. La Teoría de Juegos es un área de las matemáticas ( altamente aplicada en Economía) la cual analiza las decisiones de los jugadores, dado su incentivo de obtener un mejor beneficio propio.
Mi hermana perdió 4 pesos. En otras palabras, 4 pesos le costó aprender la lección de que, apostar sin conocer lleva a la pérdida. Para tomar decisiones, hay que saber como evaluar los riesgos.
Al final, la comisión de Juego Familiar ( mi mamá) alegó que una menor de edad no debería estar apostando y confiscó las ganancias del casino.
Conclusiones: No vuelvo a montar mi casino clandestino en casa.
